Categories &
Functions List
- bim1a_advection_diffusion
- bim1a_advection_upwind
- bim1a_axisymmetric_advection_diffusion
- bim1a_axisymmetric_advection_upwind
- bim2a_advection_diffusion
- bim2a_advection_upwind
- bim2a_axisymmetric_advection_diffusion
- bim2a_axisymmetric_advection_upwind
- bim3a_advection_diffusion
- bim3a_osc_advection_diffusion
- bim1a_laplacian
- bim1a_axisymmetric_laplacian
- bim2a_laplacian
- bim2a_axisymmetric_laplacian
- bim3a_laplacian
- bim3a_osc_laplacian
- bim1a_reaction
- bim1a_axisymmetric_reaction
- bim2a_reaction
- bim2a_axisymmetric_reaction
- bim3a_reaction
- bim1a_rhs
- bim1a_axisymmetric_rhs
- bim2a_rhs
- bim2a_axisymmetric_rhs
- bim3a_rhs
- bim2a_boundary_mass
- bim2a_axisymmetric_boundary_mass
- bim3a_boundary_mass
Function Reference: bim2a_laplacian
- Function File: A = bim2a_laplacian (mesh,epsilon,kappa)
Build the standard finite element stiffness matrix for a diffusion problem.
The equation taken into account is:
- div (epsilon * kappa grad (u)) = f
where epsilon is an element-wise constant scalar function, while kappa is a piecewise linear conforming scalar function.
See also: bim2a_rhs, bim2a_reaction, bim2a_advection_diffusion, bim1a_laplacian, bim3a_laplacian
Source Code: bim2a_laplacian
Example: 1
m = msh2m_structured_mesh (0:.1:2*pi, 0:.1:2*pi, 1, 1:4, 'random');
m = bim2c_mesh_properties (m);
kappa = 2 + sin (m.p(1, :)');
f = kappa .* cos (m.p(2, :)');
uex = cos (m.p(2, :)');
A = bim2a_laplacian (m, 3./(sum(1./kappa(m.t(1:3, :)), 1)), 1);
b = bim2a_rhs (m, 1, f);
dnodes = bim2c_unknowns_on_side (m, 1:4);
inodes = setdiff (1:columns(m.p), dnodes);
u = uex;
u(inodes) = A(inodes, inodes) \ (b(inodes)-A(inodes, dnodes) * u(dnodes));
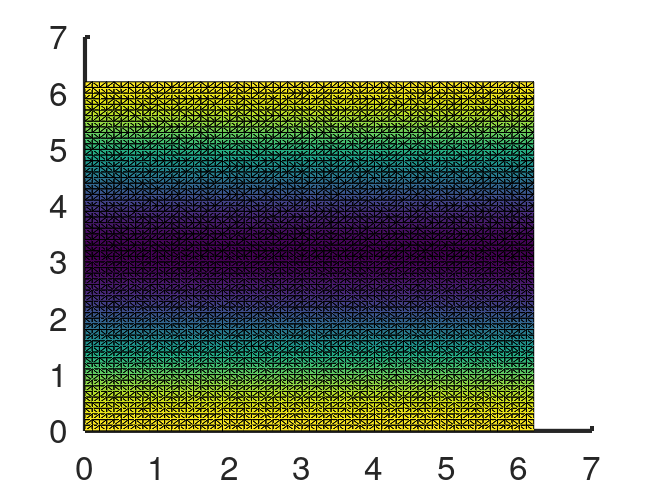
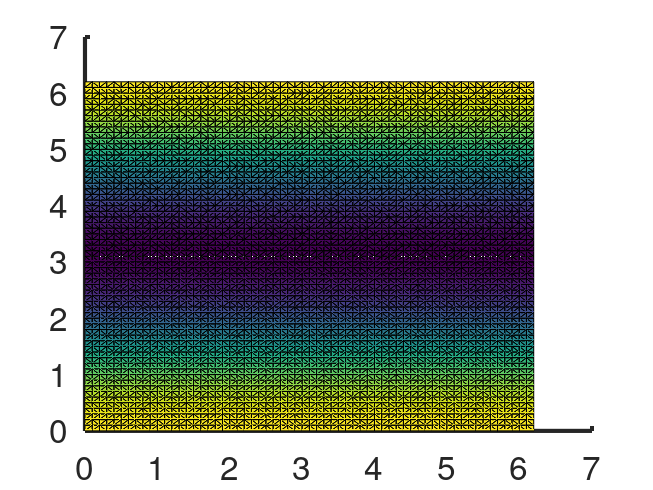
h = pdesurf (m.p, m.t, u)
figure
pdesurf (m.p, m.t, uex)
h = -39.365
|